
The difference is that now we not only talk about the point of the interval, we are including the point of the value of the function, his serves as an additional visual aid to reinforce the domain restrictions on each function. A closed circle indicates that the point is included in the interval An open circle indicates that the point is not included in the interval Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals. Intervals: To denote the edges of the loops, we are using the same notation as for the intervals of the solutions of the inequalities, remember? As you move each slider, constants and coefficients in the functions are changed, and thus the graphs of each function move to satisfy the new parameters. The following GeoGebra lab features several rational functions whose domains are defined by sliders.
Sometimes, you’ll be given piecewise functions and asked to evaluate them in other words, find the \(y\) values when you are given an \(x\) value.Lesson Objective: This interactive lesson to help students understand of piecewise-defined functions.ĭefinition: A piecewise function is a function that consists of two or more standard functions defined on different domains. See, not so bad, right? Evaluating Piecewise Functions \(\displaystyle f\left( x \right)=\left\\) graph, we can just use a closed circle as if it appears on both functions. Note that there is an example of a piecewise function’s inverse here in the Inverses of Functions section. Thus, the \(y\)’s are defined differently, depending on the intervals where the \(x\)’s are. The easiest way to think of them is if you drew more than one function on a graph, and you just erased parts of the functions where they aren’t supposed to be (along the \(x\)’s). Piecewise functions (or piece-wise functions) are just what they are named: pieces of different functions (sub-functions) all on one graph.
PIECEWISE DEFINED FUNCTION CALCULATOR HOW TO
Introduction to Piecewise Functions Absolute Value as a Piecewise Function Evaluating Piecewise Functions Transformations of Piecewise Functions Graphing Piecewise Functions Piecewise Function Word Problems How to Tell if a Piecewise Function is Continuous or Non-Continuous More Practice Obtaining Equations from Piecewise Function Graphs Introduction to Piecewise Functions
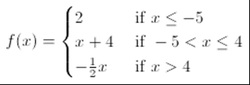
Rational Functions, Equations, and Inequalities.Solving Systems using Reduced Row Echelon Form.The Matrix and Solving Systems with Matrices.Advanced Functions: Compositions, Even and Odd, and Extrema.Solving Radical Equations and Inequalities.Solving Absolute Value Equations and Inequalities.Imaginary (Non-Real) and Complex Numbers.Solving Quadratics by Factoring and Completing the Square.Introduction to Multiplying Polynomials.Scatter Plots, Correlation, and Regression.Algebraic Functions, including Domain and Range.Systems of Linear Equations and Word Problems.Introduction to the Graphing Display Calculator (GDC).Direct, Inverse, Joint and Combined Variation.Coordinate System and Graphing Lines, including Inequalities.



 0 kommentar(er)
0 kommentar(er)
